수학 공식

앱실론 - 델타 논법

열린 구간 D에 대해서 (열린 구간은 (-5, 5) 같이 소괄호로 감싸며 -5 보다 크고 5보다 작은 수. 즉 -5, 5가 포함되지 않는 수를 의미)

$\mathrm{\forall }ϵ$ 에서의 $\mathrm{\forall }$(forall)은 존재할 수 있는 모든 값을 의미한다.

$\text{exist}\delta$에서의 $\text{exist}$(exist)는 하나 이상 존재하는 어떤 수를 의미하는 것이다.

존재할 수 있는 모든 수 중 0보다 큰 $ϵ$ 과 0보다 큰 어떠한 값 $\delta$를 의미함.

s.t. 은 such that의 줄임말로써 A s.t. B는 B를 만족하는 A 를 의미함.

$ϵ$에게 주어진 치역의 범위$|f(x)-L|<ϵ$ 는 즉 $L-ϵ<f(x)<L+ϵ$ 이고 이는

$f(x)$에서 $L$ 까지의 거리가 $\epsilon$ 보다 작다는 뜻이다.

안에 공역을 온전히 대응 시킬 수 있는 정의역 $0<\mid x-a\mid <\delta$

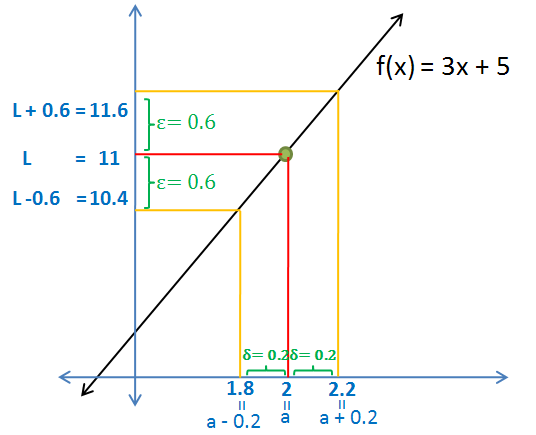
어떠한 양수 $ϵ$이 주어질때 어떠한 양수 $\delta (=\delta (\epsilon ))$가 있어서 $a$와 같지 않은 $x$가 $a-\delta$와 $a+\delta$ 사이에 있는 값이라면 $f(x)\in (L-\epsilon ,L+\epsilon )f(x)\in (L-\epsilon ,L+\epsilon )$ 라는 뜻이다.

예제를 통해 보자

$f(x)=3x+5일때\underset{x\to 2}{lim}f(x)=11을증명하라.$

$|3x+5-11|<ϵ$ 일때 $|x-2|<\delta$

이를 풀면

$|x-2|<ϵ/3,|x-2|<\delta$

이는 그래프로 다음과 같이 나타낼 수 있다.